题目链接:
题意:给出一个n×m的矩阵,位置(i。j)有一个非负权值。
每一个点仅仅能经过一次。求从(1。1)到(n。m)权值总和最大的和。还需输出路径。
思路:由于走的点越多越好,所以得到规律,当n,m随意一个为奇数时。均能够走全然部点。
当n,m全为偶数时,当点(i。j)的i和j不同奇偶时,则除了(i,j)这个点均能够走完剩下的全部点。
剩下模拟就可以。
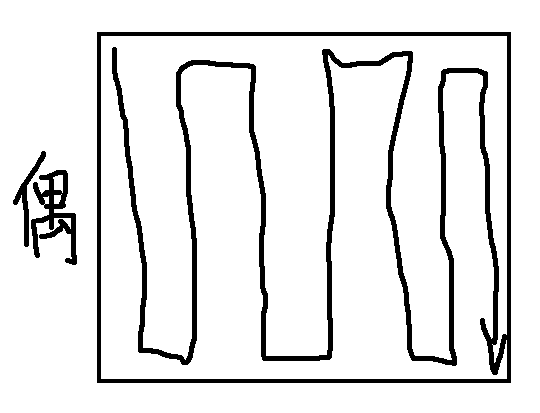
- n,m当中一个为奇数的时候,相似下图走法就可以。顺着偶数边走,若均为奇数,则随意都可。
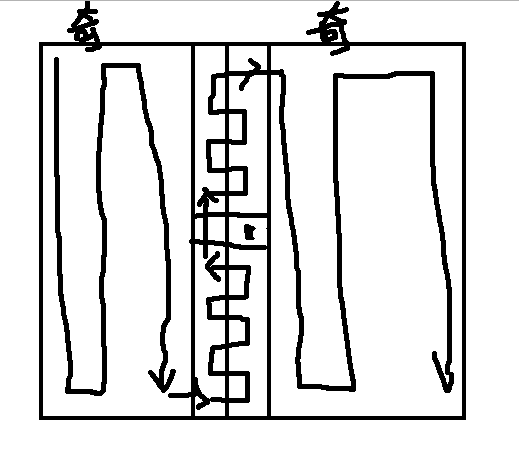
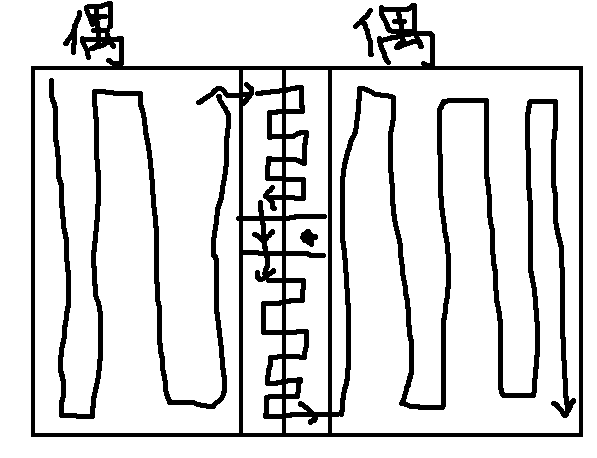
- n。m均为偶数,先找出最小的位置(ni,nj)且ni和nj奇偶不同的位置(下图中(ni,nj)为黑点位置)。
- 假设nj为奇数,相似下图走法就可以。
- 假设nj为偶数,相似下图走法就可以。
- 特别的是nj为1的时候由于不能向左分出一列。所以向右分出一列。特判就可以。
- 假设nj为奇数,相似下图走法就可以。
代码。
#include#include #include #include #include #include #include using namespace std;const int N = 1e2 + 10;void out(int n, int m, char a, char b, char c) { for (int i = 1; i <= n; i++) { if (i > 1) printf("%c", a); for (int j = 1; j < m; j++) { if (i & 1) printf("%c", b); else printf("%c", c); } }}int main() { int n, m; while (scanf("%d%d", &n, &m) != EOF) { int ans = 0, tmp = 10005; int ni, nj; for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { int x; scanf("%d", &x); ans += x; if (((i + j) & 1) && x < tmp) { tmp = x; ni = i; nj = j; } } } if (n % 2 == 0 && m % 2 == 0) ans -= tmp; printf("%d\n", ans); if (n & 1) { out(n, m, 'D', 'R', 'L'); } else if (m & 1) { out(m, n, 'R', 'D', 'U'); } else { if (nj == 1) { if (ni - 1 > 0) { out(ni - 1, 2, 'D', 'R', 'L'); printf("D"); } if (ni < n) { printf("D"); out(n - ni, 2, 'D', 'L', 'R'); } if (m > 2) { printf("R"); out(m - 2, n, 'R', 'U', 'D'); } printf("\n"); continue; } if (nj & 1) { if (nj - 2 > 0) { out(nj - 2, n, 'R', 'D', 'U'); printf("R"); } if (n - ni > 0) { out(n - ni, 2, 'U', 'R', 'L'); printf("U"); } if (ni - 1 > 0) { printf("U"); out(ni - 1, 2, 'U', 'R', 'L'); } if (m - nj > 0) { printf("R"); out(m - nj, n, 'R', 'D', 'U'); } } else { if (nj - 2 > 0) { out(nj - 2, n, 'R', 'D', 'U'); printf("R"); } if (ni - 1 > 0) { out(ni - 1, 2, 'D', 'R', 'L'); printf("D"); } if (ni < n) { printf("D"); out(n - ni, 2, 'D', 'R', 'L'); } if (m - nj > 0) { printf("R"); out(m - nj, n, 'R', 'U', 'D'); } } } printf("\n"); } return 0;}